Brunn–Minkowski theorem
In mathematics, the Brunn–Minkowski theorem (or Brunn–Minkowski inequality) is an inequality relating the volumes (or more generally Lebesgue measures) of compact subsets of Euclidean space. The original version of the Brunn–Minkowski theorem (Hermann Brunn 1887; Hermann Minkowski 1896) applied to convex sets; the generalization to compact nonconvex sets stated here is due to L.A. Lyusternik (1935).
Contents |
Statement of the theorem
Let n ≥ 1 and let μ denote the Lebesgue measure on Rn. Let A and B be two nonempty compact subsets of Rn. Then the following inequality holds:
where A + B denotes the Minkowski sum:
Remarks
The proof of the Brunn–Minkowski theorem establishes that the function
is concave in the sense that, for every pair of nonempty compact subsets A and B of Rn and every 0 ≤ t ≤ 1,
For convex sets A and B, the inequality in the theorem is strict for 0 < t < 1 unless A and B are homothetic, i.e. are equal up to translation and dilation.
See also
- Isoperimetric inequality
- Milman's reverse Brunn–Minkowski inequality
- Minkowski–Steiner formula
- Prékopa–Leindler inequality
- Vitale's random Brunn–Minkowski inequality
References
- Brunn, H. (1887). Über Ovale und Eiflächen. Inaugural Dissertation, München.
- Fenchel, Werner; Bonnesen, Tommy (1934). Theorie der konvexen Körper. Ergebnisse der Mathematik und ihrer Grenzgebiete. 3. Berlin: 1. Verlag von Julius Springer.
- Fenchel, Werner; Bonnesen, Tommy (1987). Theory of convex bodies. Moscow, Idaho: L. Boron, C. Christenson and B. Smith. BCS Associates.
- Dacorogna, Bernard (2004). Introduction to the Calculus of Variations. London: Imperial College Press. ISBN 1-86094-508-2.
- Heinrich Guggenheimer (1977) Applicable Geometry, page 146, Krieger, Huntington ISBN 0882753681 .
- Lyusternik, Lazar A. (1935). "Die Brunn–Minkowskische Ungleichnung für beliebige messbare Mengen". Comptes Rendus (Doklady) de l'académie des Sciences de l'uRSS (Nouvelle Série) III: 55–58.
- Minkowski, Hermann (1896). Geometrie der Zahlen. Leipzig: Teubner.
- Ruzsa, Imre Z. (1997). "The Brunn–Minkowski inequality and nonconvex sets". Geometriae Dedicata 67 (3): pp. 337–348. doi:10.1023/A:1004958110076. MR1475877.
- Rolf Schneider, Convex bodies: the Brunn-Minkowski theory, Cambridge University Press, Cambridge, 1993.
![[ \mu (A %2B B) ]^{1/n} \geq [\mu (A)]^{1/n} %2B [\mu (B)]^{1/n},](/2012-wikipedia_en_all_nopic_01_2012/I/e54d431eaf9d83cb831971f69e87fe7e.png)
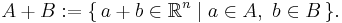
![A \mapsto [\mu (A)]^{1/n}](/2012-wikipedia_en_all_nopic_01_2012/I/b2a591258fcfa857e9ee823c04e0832d.png)
![\left[ \mu (t A %2B (1 - t) B ) \right]^{1/n} \geq t [ \mu (A) ]^{1/n} %2B (1 - t) [ \mu (B) ]^{1/n}.](/2012-wikipedia_en_all_nopic_01_2012/I/9ea5158ba3129883268349babcf52cd2.png)